Knots are the basic objects studied in the mathematical field of knot theory. Knot theory studies entanglement in closed chains, although the ideas can be extended to characterize knotting in open chains (which we describe more below). Several types of knots have been found so far in proteins. These are known and denoted as follows: trefoil (denoted also as 31), figure-8 (denoted 41), 52, and Stevedore’s knot (denoted 61). An unknotted loop is called the trivial knot, or the unknot, and is denoted 01. In the notation above, the first number denotes the minimal number of crossings a given knot can show in a projection (e.g. minimal number of crossings in a projection of a trefoil onto a plane is 3). The 31, 52 and 61 knots are chiral, i.e. they differ from their mirror images, and their complete characterization requires the determination of their chirality, which we denote by a plus (+) or a minus (-) sign next to the symbol of a knot. The 41 knot is an example of an achiral knot, i.e. it is identical to its mirror image and cannot be assigned a chirality. Knots are defined uniquely on closed chains. To define them in open chains (which have loose ends), such as proteins, one must choose how to connect the two loose ends, so that a closed chain is formed [1]. Making this choice in the most optimal way is the first difficulty we have to overcome when analyzing proteins; various ways how to form a close loop are discussed in [2]. Once this problem is addressed and an open chain is effectively transformed into a closed chain, we detect a knot type by computing a polynomial knot invariant known as Alexander polynomial. This polynomial can be calculated from a planar diagram of a knot (obtained from a projection of a knot on some two-dimensional plane). Alexander polynomial is different for all prime knots with eight or fewer crossings, which is sufficient to detect knots which appear in proteins (the most complicated knot found in proteins until now has six crossings).
| Knot type | 01 | 31 | 41 | 51 | 52 | 61 |
 unknotted |
 trefoil knot |
 figure-8 knot |
 cinquefoil knot |
 three-twist knot |
 Stevedore knot |
|
| Values of Alexander polynomial | Δ(01) = 1 | Δ(31) = 1 - t + t2 | Δ(41) = -1 + 3t - t2 | Δ(51) = 1 - t + t2 - t3 + t4 | Δ(52) = 2 - 3t + 2t2 | Δ(61) = -2 + 5t - 2t2 |
It is nontrivial to define the concept of knotting for an open chain [1]. Only in the case of a closed chain the knot type is uniquely determined, and the techniques for classifying the knotting in open chains rely on closing the chain. However, for open chains the knot type can change depending on the way the chain is closed [2]. To characterize knotting specified by a rigid trajectory of an open chain and not by the particular way the chain is closed, one strategy is to pass from a deterministic to a probabilistic concept of knotting and ask a question: what is the most likely closed knot type specified by a given rigid trajectory of an open chain. To answer this question one might try to consider all possible closures of a given chain and analyze the frequency with which different knots result from such closures. Testing of all possible closures is practically impossible but there are closure methods that do not introduce a bias in the observed frequency of various knots. In the KnotProt database, we apply a random closure method, i.e. we connect protein endpoints several hundred times to two points randomly chosen from a set of vertices of the truncated icosahedron (i.e. a polyhedron representing e.g. the geometry of C60 fullerene) positioned on a large sphere enclosing the analyzed chain. Subsequently these two points are connected by an arc lying on the surface of the sphere. The most frequently observed knot type for a given analyzed chain is then associated with that chain as its dominant knot type.
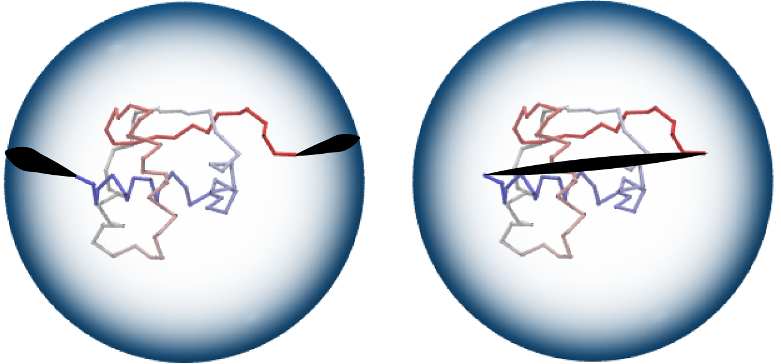
Fig 2. One method to form a closed chain is the random closure (left): two random points on a large sphere are randomly chosen and connected by line segments to the endpoints of a chain, and to each other by an (auxiliary) arc. Alternatively, it is possible to choose the direct closure method (right), which connects chain end-points by the shortest interval.
The knot types resulting from individual closures are determined by computing polynomial knot invariants. For quick computations of all analyzed subchains we use the Alexander polynomial. To detect chirality of formed knots the HOMFLY polynomial is calculated for some of the analyzed subchains.
Computing knot polynomials is relatively fast for short chains, however it can be a very time consuming process for long chains (e.g. for proteins with more than 500 amino acids – and the longest chain analyzed by the KnotProt included 3303 aminoacids). Therefore, before computing the Alexander polynomial for a given chain (or fixed subchain), after closing terminals (for each random closure separately) we first reduce it to a shorter configuration using the KMT algorithm [4]. This algorithm analyzes all triangles in a chain made by three consecutive amino acids, and removes the middle amino acid in case a given triangle is not intersected by any other segment of the chain. In effect, after a number of iterations, the initial chain is replaced by (much) shorter chain of the same topological type.
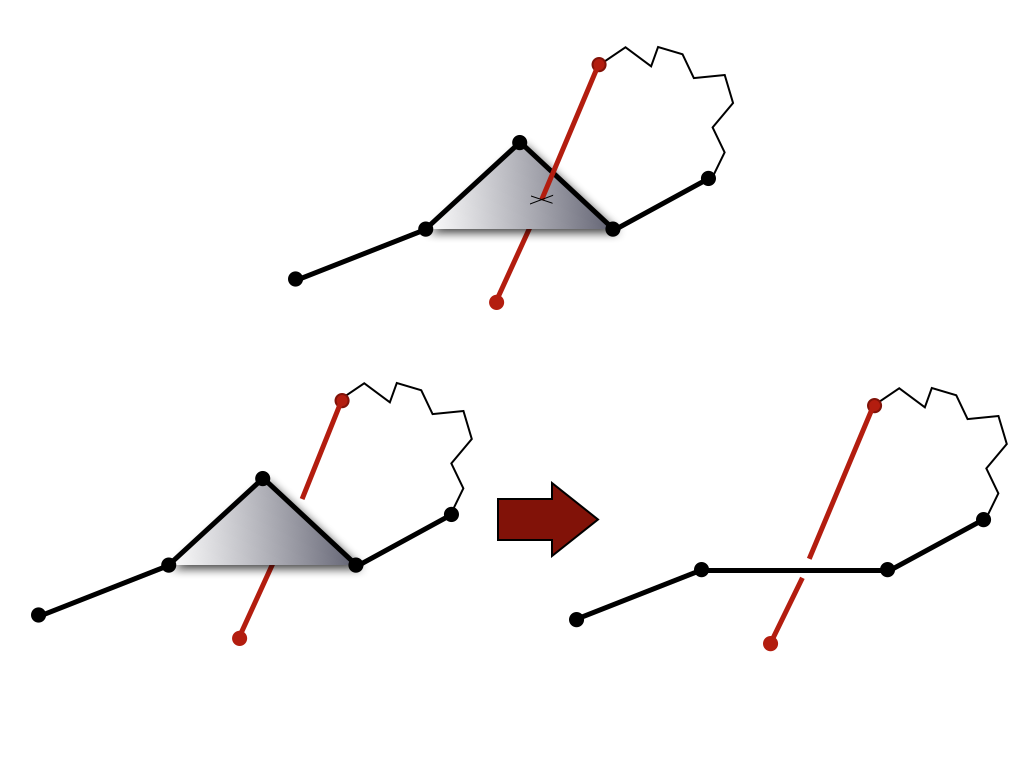
Fig 1. The KMT algorithm analyses all triangles of the protein chain, which involve three consecutive atoms. If a given triangle is not intersected by any other segment of the chain, its middle atom can be removed (bottom panel). This atom cannot be removed in the configuration in the top panel.
The KnotProt database verifies not only if a given chain is knotted (or not), but it also analyzes all subchains of a given chain. This means that for a chain of length N, we analyze all subchains spanned between atoms (aminoacids) k and l (with 1 ≤ k < l ≤ N). For a given protein this information is presented in the database within the panel “Knotting data”, in the form of an interactive “knotting fingerprint” (matrix diagram). More details how to interpret these diagrams are given in section Knotting data.
