A lot of information can be deduced from the results of trajectory analysis. For example, the results of the “fast analysis” (existence of a knot at each time step) can be used to characterize probability of knot occurrence in various reaction coordinates, such as native contacts (Q, number of contact existing in protein in native state) or RMSD. As an example, the figure below shows a plot of probability of knot occurrence P(K)=0.5 (black line) superimposed on free energy F(Q,RMSD) (right panel) for a knotted protein 2ouf (constructed in [4]) shown in the middle (figures from the paper [1]).
Fig 1. Schematic representation (left) of a knot in 2ouf protein (middle). Panel on the right presents free energy landscape of this protein measured by the fraction of native contacts formed Q and RMSD for 2ouf; black curve represents a probability of finding a knot P(K)=0,5.
As another application, the results of detailed analysis can be used to analyze knots and slipknots from the viewpoint of thermodynamics processes, as discussed in [1]. Based on such analysis, figures like those below (from [1]) can be plot. These figures show knotting, folding, and unfolding events observed for 2ouf. Trajectory insets show (top left) random knotting by the C-terminal, (top middle) folding via knotting at low Q (unique to 2ouf), and (top right) unknotting and unfolding by unplugging the N-terminal. Corresponding protein configurations are shown next to the insets. In the bottom inset, the topological signature of the protein measured by the position of the knot along the sequence is shown, with knot termini denoted by blue and red dots.
Yet another application amounts to describing the evolution of a knot when a protein is stretched by AFM or optical tweezers, as discussed in [2], and shown in figure below. This figure (from [2]) shows unraveling of the protein (left panel) at constant speed (found based on structure based model). The upper part presents unfolding curves of force versus pulling spring F(d). The lower part of the figure presents sequential movement of knot’s ends during the knot-tightening process corresponding to the unfolding curve shown above.
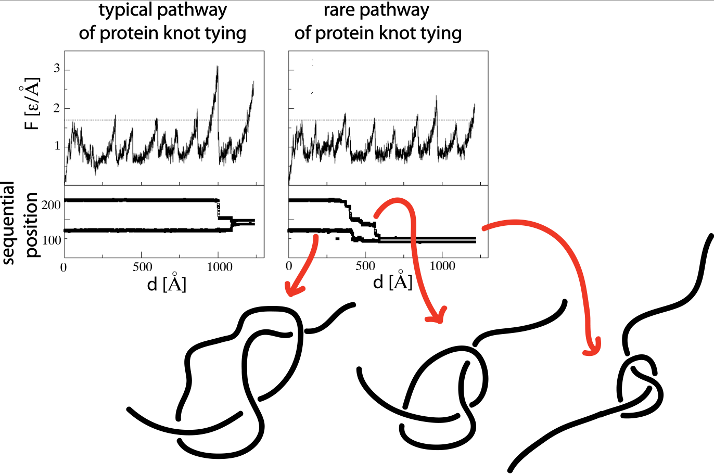
Fig 3. Unfolding curves of force versus pulling spring F(d) and corresponding sequential movement of knot’s ends during the knot-tightening process.
Finally, the trajectory analysis can be used to find optimal direction of pulling the protein to untie it. Behavior of protein configuration pulled in different directions is shown in figure below (from [3]), where, first of all, attachments points (p2, p1) are shown that may lead to an unknotted configuration at various temperatures (denoted by colors, as indicated on the scale above). Below on the right, a distribution of the knot end locations, (k2,k1) is shown. The color scale indicates the probability of attaining particular values of k2 and k1. The framed part in the right panel indicates the region covered by the left panel.
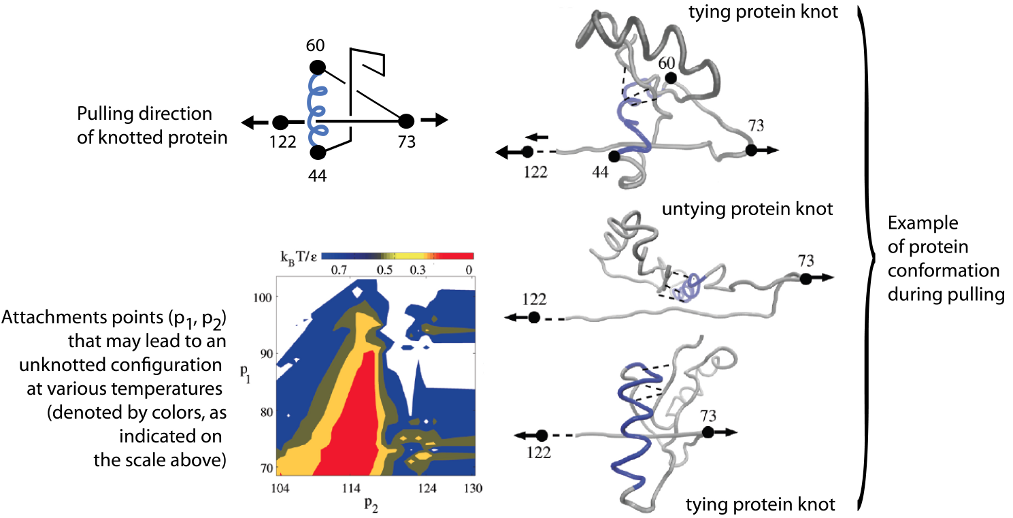
Fig 4. Stretching protein in various directions by pulling different pairs of amino acids.
It is well known that cysteine bonds introduce additional stability to protein structures [5,6,7]. Moreover the analysis of proteins with links revealed that non-trivial topology introduces additional stability [8]. Possibly, this non-trivial topology explains the exceptional stability of other proteins with similar topology, such as Cerato-platanins which has been shown to be stable up to 76oC [9], or Fungal endoglucanase (1HD5) which is stable after heating in 60o C and in pH between 3.0-11.0 [10], retaining 45% of activity after incubating for 5 minutes in 95o C [10]. The animal endoglucanase (PDB code 1WC2) withstands heating for 10 minutes in 100o C without irreversible loss of activity [11]. All proteins with links can be found in LinkProt database [12]. Yet anther example are cyclotides [13]. It has been shown that the circular protein backbone and knotted arrangement of disulfide bonds make so called cyclotides also exceptionally stable [7]. Following the example given in cyclotides webpage, “In their native medicine uses, for example, the peptides are boiled when the plant Oldenlandia affinis is used to make a tea that women ingest to accelerate childbirth“ [14]. These peptides are exceptionally stable to enzymatic degradation [7,15]. Such peptides due to their stability are commonly used as templates in pharmaceutical applications (including anti-HIV, anti-bacterial and insecticidal activity [7,15]).
Collected in the KnotProt 2.0 proteins with knots formed based on cysteines or ions bonds together with protein backbone can be used:
Figure 4 shows two out of three identified trefoil knots in a coagulogen, the clotting protein from horseshoe crab: a structural homologue of nerve growth factor (DPB 1aoc chain A). Topological characterization of this protein uncovers its hidden complexity.
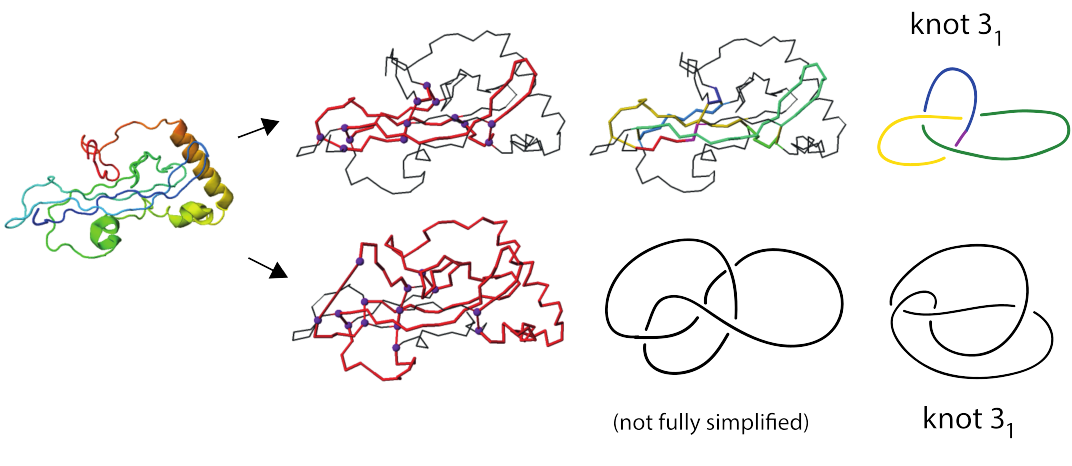
Fig 5. Cartoon representation of the clotting protein from horseshoe crab, left. The structures on the right show two different trefoil knots identified based on disulfide bonds and protein backbone. Magenta spheres indicate positions of the cyteines which form disulfide bonds.
[1] Sulkowska JI, Noel JK, Onuchic JN (2012) Energy landscape of knotted protein folding, PNAS 109, 17783-8.
[2] Sulkowska JI, Sulkowski P, Szymczak P, Cieplak M (2008) Stabilizing effect of knots on proteins, PNAS 105, 19714-9.
[3] Sulkowska JI, Sulkowski P, Szymczak P, Cieplak M (2010) Untying knots in proteins, J. Am. Chem. Soc. 132, 13954-6.
[4] King NP, Jacobitz AW, Sawaya MR, Goldschmidt L, Yeates TO (2010) Structure and folding of a designed knotted protein, PNAS 107, 20732–7.
[5] Inglis AS, Liu TY (1970) The stability of cysteine and cystine during acid hydrolysis of proteins and peptides, J. Biol. Chem. 245, 112-6
[6] Maulik VT, Jennifer SL, Teruna JS (2009) The role of thiols and disulfides in protein chemical and physical stability, Curr. Protein Pept. Sci. 10, 614-25
[7] Craik DJ, Simonsen S, Daly NL (2002) The cyclotides: novel macrocyclic peptides as scaffolds in drug design, Curr. Op. Drug Disc. Dev. 5, 251-260
[8] Dabrowski-Tumanski P, Sulkowska JI (2017) Topological knots and links in proteins, PNAS, 114, 3415-20
[9] de Oliveira AL, Gallo M, Pazzagli L, Benedetti CE, Cappugi G, Scala A, Pantera B, Spisni A, Pertinhez T, Cicero DO (2011) The structure of the elicitor cerato-platanin (CP), the first member of the CP fungal protein family, reveals a double alpha/barrel fold and carbohydrate binding, J. Biol. Chem. 286, 17560-8
[10] Hayashida S, Ohta K, Mo K (1988) Cellulases of Humicola insolens and Humicola grisea, Methods Enzymol. 160, 323-32
[11] Xu B, Hellman U, Ersson B, Janson JC (2000) Purification, characterization and aminoacid sequence analysis of a thermostable, low molecular mass endo- beta-1,4-glucanase from blue mussel, Mytilus edulis. Eur. J. Biochem. 267, 4970-7
[12] Dabrowski-Tumanski P, Jarmolinska AI, Niemyska W, Rawdon EJ, Millett KC, Sulkowska JI (2016) LinkProt: A database collecting information about biological links, Nucleic acids research 45, D243–9.
[13] Craik DJ, Daly NL, Bond T, Waine C (1999) Plant cyclotides: A unique family of cyclic and knotted proteins that defines the cyclic cystine knot structural motif, J. Mol. Biol. 294, 1327-36.
[14] Gran L (1973) Isolation of oxytocic peptides from Oldenlandia affinis by solvent extraction of tetraphenylborate complexes and chromatography on sephadex LH-20, Lloydia 36, 207-8
[15] Jennings C, West J, Waine C, Craik D, Anderson M (2001) Biosynthesis and insecticidal properties of plant cyclotides - the cyclic knotted proteins from O. affinis, PNAS 98, 10614-9
